1551. Correcting parenthesization
Given a
string of parentheses, we must turn it into a well formed string by changing as
few characters as possible (we cannot delete or insert characters).
There are
three kinds of parentheses: regular (), brackets [] and curly brackets {}. Each
pair has an opening ('(', '[' and '{' respectively) and a closing (')', ']' and
'}') character.
A well
formed string of parentheses is defined by the following rules:
·
The empty string is well formed.
·
If s is a
well formed string, (s), [s] and {s} are well formed strings.
·
If s and t are well formed strings, the
concatenation st is a well formed
string.
As
examples, "([{}])", "" and "(){}[]" are well
formed strings and "([}]", "([)]" and "{" are
malformed strings.
For the
given string of parentheses find the minimum number of characters that need to
be changed to make it into a well formed string.
Input. Each line contains the string with even number
of symbols '(', ')', '[', ']', '{', '}'. The length of each line is no more
than 50.
Output. For each input string print in a
separate line the minimum number of characters that need to be changed to make
it into a well formed string.
|
Sample input |
Samle output |
|
]()[((() ([)] ([{}[] |
3 2 1 |
SOLUTION
dynamic programming
Algorithm analysis
Let f(i, j)
be the smallest
number of characters that can be changed so that the substring sisi+1…sj-1sj becomes correct.
Then the following statements hold:

Function enc(si ,sj) returns:
a)
0, if the characters si
and sj are matching
opening and closing parentheses;
b)
2, if si is a closing parenthesis and sj is an opening parenthesis;
c) 1 otherwise. In this case,
it is enough to change one of the symbols si or sj so that
they form the correct pair of parenthesis;
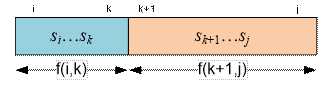
![]() (f(i, k) + f(k + 1, j)). Consider the sequence sisi+1…sj-1sj as a sequence of two
regular parenthesis structures: si…sk è sk+1…sj.
The
length of a substring si…sk must be even, hence k takes the values i +
1, i + 3, …, j – 2.
(f(i, k) + f(k + 1, j)). Consider the sequence sisi+1…sj-1sj as a sequence of two
regular parenthesis structures: si…sk è sk+1…sj.
The
length of a substring si…sk must be even, hence k takes the values i +
1, i + 3, …, j – 2.
Example
Consider the first line
from the sample.
f(0, 7) = f(0, 3) +
f(4, 7) = (2 + f(1, 2)) + (0 + f(5, 6)) = (2 + 0) + (0 + 1) = 3
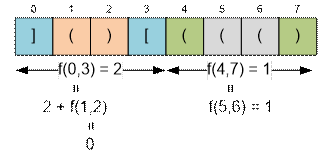
Algorithm realization
Store
the values of f(i, j) in m[i][j]. Read
the input string into s.
int m[51][51], res;
string s;
Implementation of the function enc(c, d).
int enc(char
c, char d)
{
string p = "([{)]}";
Function returns 2 if c is a closing parenthesis and d is an opening parenthesis.
if (p.find(c)
/ 3 > 0 && p.find(d) / 3 < 1) return
2;
Function returns 0, if c and d are the corresponding
parentheses. If they are not in the correct order, the function will return the
value 2 above.
if (p.find(c)
% 3 == p.find(d) % 3 && c != d) return
0;
In all other cases, return 1.
return 1;
}
Function f(i,
j) returns the smallest number of
characters that can be changed so that the substring sisi+1…sj-1sj becomes valid.
int f(int
i, int j)
{
if (i > j)
return 0;
if (m[i][j] != -1) return m[i][j];
int r =
f(i+1,j-1) + enc(s[i],s[j]);
for(int k = i + 1; k < j; k += 2)
r = min(r,f(i,k) + f(k+1,j));
return
m[i][j] = r;
}
The main part of the program. Process multiple test cases.
while(cin
>> s)
{
memset(m,-1,sizeof(m));
The answer to the problem is the value f(0, |s| – 1), where s is the
input string.
res = f(0, s.size() - 1);
cout << res << endl;
}
Java realization
import java.util.*;
public class Main
{
static int m[][];
static String s;
public static int enc(char c, char d)
{
String p = "([{)]}";
if (p.indexOf(c) / 3 > 0 && p.indexOf(d) / 3 < 1) return 2;
if (p.indexOf(c) % 3 == p.indexOf(d) % 3 && c != d) return 0;
return 1;
}
public static int f(int i, int j)
{
if (i > j) return 0;
if (m[i][j] != -1) return m[i][j];
int r = f(i + 1, j - 1)
+ enc(s.charAt(i), s.charAt(j));
for (int k = i + 1; k < j; k += 2)
r = Math.min(r, f(i, k) + f(k + 1, j));
return m[i][j] = r;
}
public static void
main(String[] args)
{
Scanner con = new Scanner(System.in);
while (con.hasNext())
{
s = con.next();
int len = s.length();
m = new int[len][len];
for(int i = 0; i < len; i++)
for(int j = 0; j < len; j++)
m[i][j] = -1;
int res = f(0, len - 1);
System.out.println(res);
}
con.close();
}
}